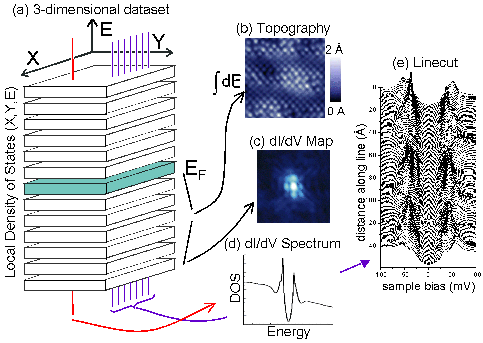
STM Measurement Types

Fig 1: (a) An STM has access to an essentially 3-dimensional dataset: two spatial dimensions (x, y) and energy E. This 3-dimensional data space can be explored in 4 different ways (b)-(e). (b) Topography: the tip height z is adjusted through a feedback loop to maintain a constant current Iset at a constant bias voltage Vset. Recording the tip height effectively maps out the height of the surface. (c) dI/dV map: the density of states at a fixed energy E is mapped as a function of position (x, y) on the sample surface. (d) dI/dV spectrum: the density of states as a function of energy is measured at a single point on the sample surface. (e) Linecut: the density of states as a function of energy is mapped at several points along a line on the sample surface.

Our STM holds the tip at virtual ground, and applies a bias voltage V to the sample. The tunneling current is measured from the tip. The tip sits at the end of a piezo tube scanner (with 4 quadrants ±x and ±y on the outside, and a single electrode for z on the inside), which can control its motion with sub-Angstrom precision in 3 directions. So we can measure tunneling current as a function of 4 variables: x, y, z, and V. In practice, we usually attempt to keep z constant by employing a feedback loop to keep the tunneling current constant at a fixed bias voltage. Assuming that z is constant, we then take measurements as a function of x, y, and V.

Topography

The most common mode of STM measurement employed by STM groups around the world is a topography. In this mode, we raster the tip across the surface at a fixed sample bias voltage V_set, and employ a feedback loop which controls the voltage on the z piezo to keep the tunneling current constant at I_set. By recording the voltage to the z piezo, we can effectively map the height of the surface.

It's actually not clear what we mean by the "height" of the surface. One obvious suggestion would be some contour of constant charge density. However, as we can see from:

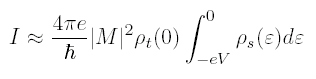
the tunneling current does not depend on the total charge density, but only the charge density within eV below the Fermi surface, where -V is the applied bias voltage.

One might argue then that we should apply an arbitrarily large voltage so that we can capture more of the charge density, but we then run into two problems: (1) Some of our samples are fragile compounds with weak bonds, and if we apply a large voltage locally, pieces of the surface will literally rip off. (2) If V is too high (on order the work function φ), our tunneling approximation breaks down.

So we are stuck with this somewhat arbitrary definition of the "height of the surface" as the tip-sample separation for which tunneling current is fixed at a particular constant value I_set for a particular applied bias voltage Vset. In practice we usually choose to fix the current at -100 pA, for a bias voltage of -100 mV. This is arbitrary, but gains some validity from the fact that we do see atoms and other structural features as expected, even over a wider range of choices of I_set and V_set. The most widely varying density of states features of the superconducting samples we have studied so far seem to be within 75 meV of the Fermi level.

Density of states

From the tunneling equation above, we see that if we hold the tip-sample separation constant, at a given (x, y) location, and put a negative bias voltage -V on the sample, we have:

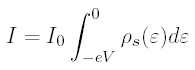
In other words, we can measure the integral of the density of states, down to any energy -eV, by varying -V. Note that for a negative bias voltage on the sample, we are tunneling electrons from sample to tip, and we are measuring the integrated density of full states below the Fermi level in the sample. For a positive bias voltage on the sample, we are tunneling electrons from tip to sample, and we are measuring the integrated density of empty states above the Fermi level in the sample.

OK, that's nice, we have the integrated density of states (IDOS). But it would be much nicer to just have the density of states (DOS). After acquiring an IDOS vs. V curve, we could take a numerical derivative of our data to get the DOS. But taking a derivative numerically is a horribly noisy thing to do. It is much better to measure the derivative directly.

So we employ a lock-in amplifier to modulate the bias voltage by dV (typically a few mV) around a DC voltage V of interest. As a result of the voltage modulation dV we can measure a current modulation dI. We call this dI/dV the conductance g(V). Now, we can write:

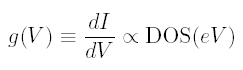
Therefore, by using a lock-in and varying V, we can map out an entire density of states curve.

The energy resolution is limited by the amplitude of the wiggle (until the modulation becomes less than approximately K_BT = 0.36 meV at T = 4.2 K). So ideally, we could make the voltage modulation smaller than 0.36 mV. But in practice, we can't get enough signal-to-noise at this low amplitude without prohibitively long averaging times. Most of our data is measured with a 2 mV RMS modulation, therefore blurring our energy resolution by approximately 5.6 meV.

Linecut

In the previous section, we discussed a single DOS curve at a single location. Since we have (x, y) control over the location of our tip using the piezo tube scanner, we can measure DOS curves anywhere we want. Some samples, like good metals (without impurities), should have a completely homogenous DOS everywhere.

But some more interesting samples are inhomogeneous. For example, we can measure a full DOS curve at every point along a straight line, spaced a few Å apart, and we see a "linecut".

DOS map

Basically what we are discussing here is a three-dimensional data set: two spatial dimensions x and y (by varying the position of the tip) and one energy dimension (by varying V). We can view this 3-dimensional data set as a series of DOS-vs-energy curves at every location (x, y), or we could view it as a series of 2-dim DOS-maps at each energy eV. Mapping the DOS at a specific energy is a good visual way to see the inhomogeneities in the density of states.